Question

A spaceship with a mass of 2.8 × 106 kg is traveling toward two spherical asteroids, each with a mass of 5.0 × 1016 kg, that are 40 km apart center-to-center. Its path is perpendicular to the line joining the asteroids and is aimed at the midpoint of that line. What is the net gravitational force exerted by the asteroids on the spaceship when the spaceship is 30 km away from that midpoint? (G = 6.67 × 10-11 N • m2/kg2)

Answer 1

Find F = Gm1m2/r²
where
G= 6.67×10^-11 N • m2/kg2
m1= 5.0×10^16 kg,
m2= 2.8×10^6 kg
and
r = ((20*10^3)²+(30*10^3)²)^(1/2)
Then,
F= 7183.07692 N
Fnet = (2)*F*cos[arctan(20/30)] = 11953 N

Answer 2

The net gravitational force exerted by the asteroids on the spaceship when the spaceship is 30 km away from that midpoint is 12000 Newtons

Step-by-step explanation:

Gravitational force is given by

`F=(Gm_1m_2)/(r^(2))`

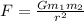
where
`m_1=2.8* 10^(6) kg,m_2=5.0* 10^(16)kg, r=[20^(2)+30^(2)]^{(1)/(2)}km=36km`

=>
`F=(6.674* 10^(-11)* 2.8* 10^(6)* 5.0* 10^(16))/(36000^(2))N=7210N`

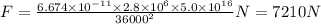
Now the force F is acting on spaceship due to two asteroids at an angle
`\Theta` with the line joining spaceship and mid-point such that
`\cos (\Theta )=(30)/(36)`

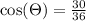
Therefore net force ,
`F_net=2F\cos (\Theta )=2* 7210* (30)/(36)N=12017 N\sim 12000 N`

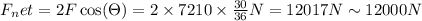
Thus the net gravitational force exerted by the asteroids on the spaceship when the spaceship is 30 km away from that midpoint is 12000 Newtons