Question

at a charity basketball game, 450 tickets were sold to students at a school. The remaining x tickets were sold to the public. The prices of the two types of tickets are shown. When all the tickets were sold, $10,500 was collected. How many tickets were sold to the public?

Answer 1

The number of tickets sold to the public was 375

Explanation:

The complete question is

At a charity basketball game, 450 tickets were sold to students at a school. The remaining x tickets were sold to the public. The students paid $15 and public $25. When all the tickets were sold, $10,500 was collected. How many tickets were sold to the public?

Let

x ----> number of tickets sold to the students

y ----> number of tickets sold to the public

we know that

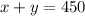`x+y=450` ----> equation A

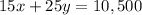`15x+25y=10,500` ----> equation B

Solve the system by graphing

The solution is the intersection point both graphs

using a graphing tool

The solution is the point (75,375)

see the attached figure

therefore

The number of tickets sold to the public was 375