Question

The ΔPQR is right-angled at P, and PN is an altitude. If QN = 12 in and NR = 6 in, find PN, PQ, PR.

Answer 1

PN = 6√2 in

PQ = 6√6 in

PR = 6√3 in

Explanation:

Please see the attached image where the triangle and the known values are labeled.

From Right triangle altitude theorem, we have

`PN=√(QN\cdot NR)\\PN=√(12\cdot6)\\PN=6\sqrt2`

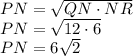
Now, in right angle triangle PNQ

`PQ=√((6\sqrt2)^2+12^2)\\PQ=√(72+144)\\PQ=√(216)\\PQ=6\sqrt6`

Similarly, in triangle PNR,

`PR=√((6\sqrt2)^2+6^2)\\PQ=√(72+36)\\PQ=√(108)\\PQ=6\sqrt3`

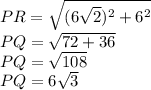
Therefore, we have

PN = 6√2 in

PQ = 6√6 in

PR = 6√3 in

Answer 2

In the right triangle PQR:
Hypotenuse: QR = QN + NR = 12 + 6 = 18 cm
PN² = QN · NR
PN² = 12 · 6 = 72
PN = √72 = √(36 · 2 ) = 6√2 cm
PQ² = (6√2)² + 12² = 72 + 144 = 216
PQ = √216 = √(36 · 6 ) = 6√6 cm
PR² = 18² - (6√6)² = 324 - 216 = 108
PR = √108 = √(36 · 3) = 6√3 cm
Answer:
PN = 6√2 cm,
PQ = 6√6 cm,
PR = 6√3 cm.