Question

Find all the zeroes of the equation 2x^4-5x^3+53x^2-125x+75=0

Answer 1

see below

Explanation:

1. -6, -2

2. 7 - √3, 2 + √6

3. 1, 3/2, +- 5i

4. s⁵+40s^4v+640s^3v^2+5,120s^2v^3+20,480sv^4+32,768v^5

5. y = x^3 +4x^2-2x-5

6. 7.5

7. 1

8. y = x^4-6x^3+6x^2-6x+5

9.x^2+2x+17=0

Answer 2

Answer: The zeroes of the equation are x=1, 3/2, 5i, -5i.

Step-by-step explanation:

Given equation
`2x^4-5x^3+53x^2-125x+75=0`

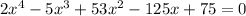
Applying rational roots theorem.

The constant term is 75 and leading coefficient is 2.

Factors of 75 are 1,3,5,15. and factors of 2 are 1, and 2.

Therefore, possible rational roots would be ±1,3,5,15,1/2, 3/2, 5/2 and 15/2.

Let us check first x=1 if it is a root or not.

Plugging x=1 in given equation, we get

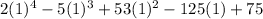`2(1)^4-5(1)^3+53(1)^2-125(1)+75` would give us 0.

Therefore, first root would be x=1 so the first factor would be x-1.

Dividing given polynomial using syntactic division

________________________

1 | 2 -5 53 -125 75

2 -3 +50 -75

_______________________

2 -3 +50 -75 0

So the other factored polynomial, we get

`2x^3-3x^2+50x-75`

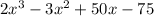
Factor it by grouping

`(2x^3-3x^2)+(50x-75)`

`x^2(2x-3) +25(2x-3)`

`(2x-3)(x^2+25).`

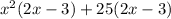
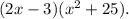
Setting each of the factors equal to 0, we get

2x-3=0

2x=3

x= 3/2.

`x^2+25 =0.`

`x^2 = -25.`

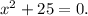
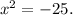
Taking square root on both sides, we get

x = ±5i

Therefore, the zeroes of the equation are x=1, 3/2, 5i, -5i.