Question

Two sides of a triangle have lengths 8 ft and 12 ft. describe the possible lengths of the third side.

Answer 1

4 < x < 20 i believe???? Not 100% sure

Answer 2

Answer: The length of the third side is greater than 4 ft and less than 20 ft.

Step-by-step explanation: Given that two sides of a triangle have lengths 8 ft and 12 ft.

We are to describe the possible lengths of the third side.

Let x ft be the length of the third side of the triangle.

We know that

the sum of the lengths of any two sides of a triangle is always greater than the third side.

So, we must have

`8+12>x\\\\\Rightarrow 20>x\\\\\Rightarrow x<20~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

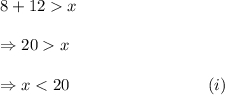
Also,

`12+x>8\\\\\Rightarrow x>8-12\\\\\Rightarrow x>-4~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

and

`8+x>12\\\\\Rightarrow x>12-8\\\\\Rightarrow x>4~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(iii)`

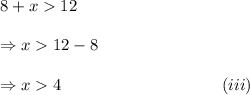
From inequalities (i), (ii) and (iii), we get

`4<x<20.`

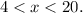
Thus, the length of the third side is greater than 4 ft and less than 20 ft.