Answer:
See below
Explanation:
A) The quadratic function that models this data is
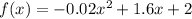 which you can view in the graph attached (done by regression).
which you can view in the graph attached (done by regression).
B)
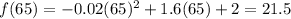 , or 21.5 miles
, or 21.5 miles
C) Set
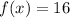 and solve for x:
and solve for x:
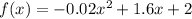
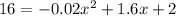
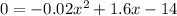


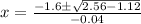

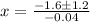
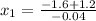
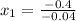

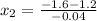
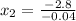
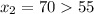
Since
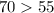 , then 10mph is the maximum speed you could drive and still reach the gas station that is 16 miles away when the speed limit is 55.
, then 10mph is the maximum speed you could drive and still reach the gas station that is 16 miles away when the speed limit is 55.