Question

(23) Geometry

Study Guide

Given triangle ABC with A(-4,-2) B (4,4) and C(18,-8)

Write the equation for the line containing perpendicular bisector of AC in point-slope form.

Answer 1

Answer:
y+5 = (11/3)(x-7)
which can be written as

`y+5 = (11)/(3)(x-7)`

----------------------------------------------

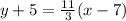
Step-by-step explanation:

A = (-4,-2)
C = (18,-8)
D = midpoint of segment AC
D = (p,q)
p = ((x coordinate of A)+(x coordinate of C))/2
p = ((-4)+(18))/2
p = 14/2
p = 7
q = ((y coordinate of A)+(y coordinate of C))/2
q = ((-2)+(-8))/2
q = -10/2
q = -5
The midpoint of segment AC is D = (p,q) = (7,-5)

Now let's find the slope of line AC
m = (y2-y1)/(x2-x1)
m = (-8-(-2))/(18-(-4))
m = (-8+2)/(18+4)
m = -6/22
m = -3/11

Flip the fraction and the sign of the slope
flip the fraction: -3/11 ----> -11/3
and flip the sign from positive to negative: -11/3 ----> +11/3 = 11/3

The answer will have a slope of 11/3 and the line goes through D = (7,-5), so using point slope form we can say:
y-y1 = m(x-x1)
y-(-5) = (11/3)(x-7)
y+5 = (11/3)(x-7)

which why the answer is
y+5 = (11/3)(x-7)
and it can be written as

`y+5 = (11)/(3)(x-7)`
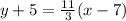
In the first version mentioned above, the 11/3 is in its own set of parenthesis to indicate to multiply all of 11/3 by the quantity (x-7). We aren't simply multiplying the 3 only.