Question

Find the following measures for this figure.

Lateral Area = 55 square units 5√(47) square units 5√(146) square units
Volume = 275 cubic units 91 2/3 cubic units 36 2/3 cubic units

Answer 1

1. We can find lateral area of a cone by
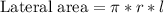`\text{Lateral area}=\pi*r*l`, where r equals radius of cone and l equals slant height of cone.

We can find slant height of our cone using Pythagorean theorem.

`l=\sqrt{11^(2)+5^(2)}`

`l=√(121+25)`

`l=√(146)`

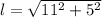
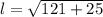
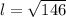
Let us substitute our slant height in lateral area formula.

`\text{Lateral area}=\pi*5√(146)`

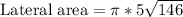
Therefore, our lateral area will be
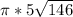`\pi*5√(146)` square units.

2.
`\text{Volume of cone}=(1)/(3) \cdot\pi\cdot r^(2)\cdot h`

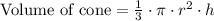
Upon substituting our given values in volume formula we will get,

`\text{Volume of cone}=(1)/(3) \cdot\pi\cdot 5^(2)\cdot 11`

`\text{Volume of cone}=(1)/(3) \cdot\pi \cdot 25\cdot 11`

`\text{Volume of cone}=(275)/(3) \cdot\pi`

`\text{Volume of cone}=91(2)/(3) \cdot\pi`

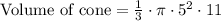
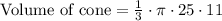
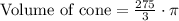
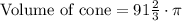
Therefore, volume of our cone will be
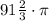`91(2)/(3) \cdot\pi` cubic units.