Answer:
0.15 rad/s
Explanation:
A rocket is launched at the rate of 11 feet per second from a point on the ground 15 feet from an observer.
To find rate of change of angle when the rocket is 30 feet above the ground
Height of rocket, y = 30 feet
Speed of rocket,

Distance of observer from rocket, d = 15 feet
Angle between observer and rocket at height 30 feet is Ф
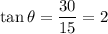
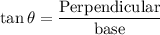
Distance between observer and rocket launch doesn't change.
So, d=15 will remain constant.
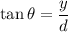
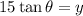
differentiate w.r.t t
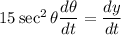

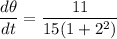

Hence, The rate of change of the angle of elevation is 0.15 rad/s