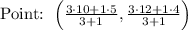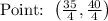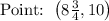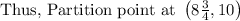Question

PLEASE HELP WILL GIVE BRAILIEST AND 10 POINTS

Point A is located at (5, 4) and point B is located at (10, 12).

What point partitions the directed line segment ​ AB¯¯¯¯¯ ​ into 3:1 ratio?




(614, 6)

(834, 10)

(8, 5)

(7, 11)

Answer 1

(8 3/4, 10)

Explanation:

I took the quiz. I hope this helps :)

Answer 2

`\text{Partition point at }\left(8(3)/(4),10\right)`

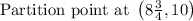
B is correct.

Explanation:

We are given point A(5,4) and point B(10,12).

We need to find point which divides line segment AB into 3:1

Using section formula of coordinate system to find coordinate

Formula:

`(x,y)\rightarrow \left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

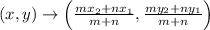
where,

`A(x_1,y_1)\rightarrow (5,4)`

`B(x_2,y_2)\rightarrow (10,12)`

`m:n\rightarrow 3:1`

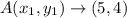
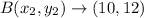
Substitute into formula and find out partition point,

`\text{Point: }\left((3\cdot 10+1\cdot 5)/(3+1),(3\cdot 12+1\cdot 4)/(3+1)\right)`

`\text{Point: }\left((35)/(4),(40)/(4)\right)`

`\text{Point: }\left(8(3)/(4),10\right)`

`\text{Thus, Partition point at }\left(8(3)/(4),10\right)`