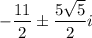Answer:
The value of x is
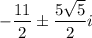
Explanation:
Given the equation
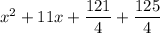
For making perfect square root
Firstly, we will half of middle term then add and subtract the square of half of the middle term in the equation
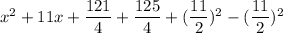
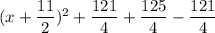
Now, the like terms will be the cancel.
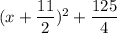
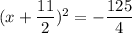
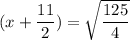
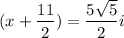
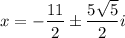
Hence, The value of x is