Question

If the equation of a circle is (x - 2)2 + (y - 6)2 = 4, it passes through point ______.

(2, 8)(5, 6)(-5, 6) (2, -8)

Answer 1

what you need to do is to plug the x and y value into the equation to see which one works.
(2-2)²+(8-6)²=0+4=4
so (2,8) is the answer.
Make sure by plugging in the other three pairs of values. You'll see that only (2,8) works.

Answer 2

The required point is (2,8).

Explanation:

Given : Equation of a circle is
`(x-2)^2+(y-6)^2=4`

To find : Point passing through the equation?

Solution :

To find the point we have to substitute each point if it satisfy teh equation then it lies on the circle.

1) (2,8) , put x=2 and y=8

`(2-2)^2+(8-6)^2=4`

`(0)^2+(2)^2=4`

`4=4`

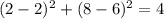
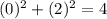
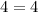
This point satisfy the equation.

2) (5,6) , put x=5 and y=6

`(5-2)^2+(6-6)^2=4`

`(3)^2+(0)^2=4`

`9\\eq4`

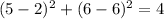
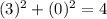
This point does not satisfy the equation.

3) (-5,6) , put x=-5 and y=6

`(-5-2)^2+(6-6)^2=4`

`(-7)^2+(0)^2=4`

`49\\eq4`

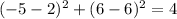
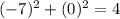
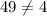
This point does not satisfy the equation.

4) (2,-8) , put x=2 and y=-8

`(2-2)^2+(-8-6)^2=4`

`(0)^2+(-14)^2=4`

`196\\eq4`

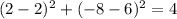
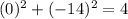
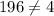
This point does not satisfy the equation.

Therefore, The required point is (2,8).