Question

(05.05 LC)

Determine whether the origin is included in the shaded region and whether the shaded region is above or below the line for the graph of the following inequality:

y < two thirds x + 2



The origin is not included in the shaded region and the shaded area is above the line.

The origin is not included in the shaded region and the shaded area is below the line.

The origin is included in the shaded region and the shaded area is above the line.

The origin is included in the shaded region and the shaded area is below the line

Answer 1

the origin is (0,0)

is it included in the shaded region.....another words, is it one solution to ur inequality...so we sub to find out...

y < 2/3x + 2.....subbing in (0,0)...x = 0 and y = 0
0 < 2/3(0) + 2
0 < 2 (this is correct)....so (0,0), the origin, is included in the shaded region...and since ur inequality sign is < (less then), it is shaded below the line

Answer 2

The origin is included in the shaded region and the shaded area is below the line

Explanation:

Given inequality,

y < two thirds x + 2

`\implies y<(2)/(3)x+2`

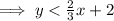
When for a point the inequality is true then we can say that the point included in the shaded region of the inequality,

At (0,0),

`0<(2)/(3)(0)+2`

`\implies 0<2`

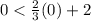
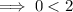
Which is true.

So, the origin is included in the shaded region.

Now, (0,0) lie below the line,

Hence, the shaded area is below the line.

Last option is correct.