Question

Which of the functions below could possibly have created this graph?

Answer 1

There are three turning points. So the highest power should be 4. Also, it approaches -infinity as x gets infinitely larger. It's negative.
Choose A

Answer 2

The function that could possibly have created this graph is:

`F(x)=(-1)/(3)x^4+7x^2+15x`

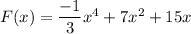
Explanation:

As we know that any odd degree polynomial has odd number of real zeros since the complex zero always exist in pair.

Here in the graph we see that there are 4 real zeros.

Hence, the polynomial can't be a odd degree polynomial.

Hence, option: B and Option: C are discarded.

So, we are left with choice A and D i.e. a even polynomial.

Also as we could see that the end behavior of the graph satisfy:

as x→ -∞ F(x) → -∞

Also when x → ∞ then F(x) → -∞

Hence, the even degree polynomial must have a negative leading coefficient.

Hence, option: D is also discarded.

Hence, option: A is the answer.