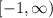Question

Sketch the plane curve represented by the given parametric equations. Then use interval notation to give the relation's domain 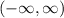and range. X = 2t, y = t2 + t + 3

Answer 1

Domain:

`(-\infty,\infty)`

Range:

`[2.75,\infty)`

Explanation:

we are given parametric equation as

`x=2t`

`y=t^2+t+3`

We can change into rectangular equation

we can eliminate t from first equation and plug into second equation

`x=2t`

`t=(x)/(2)`

now, we can plug that into second equation

`y=((x)/(2))^2+(x)/(2)+3`

now, we can draw graph

Domain:

we know that

domain is all possible values of x for which any function is defined

we can see that our equation is parabolic

and it is defined for all values of x

so, domain will be

`(-\infty,\infty)`

Range:

we know that

range is all possible values of y

we can see that

smallest y-value is 2.75

so, range will be

`[2.75,\infty)`

Answer 2

Domain:
`( -\infty,\infty )` and Range:
`[ -1,\infty )`

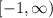
Explanation:

We have the parametric equations
`x= 2t` and
`y=t^(2)+t+3`.

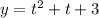Now, we will find the values of 'x' and 'y' for different values of 't'.

t : -3 -2.5 -2 -1.5 -1 0 1 1.5 2

`x= 2t` : -6 -5 -4 -3 -2 0 2 3 4

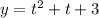`y=t^(2)+t+3` : 9 6.75 5 3.75 3 3 5 6.75 9

Now, we can see that these parametric equations represents a parabola.

The general form of the parabola is
`y=ax^(2)+bx+c`.

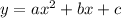Now, we have the point ( x,y ) = ( 0,3 ). This gives that c = 3.

Also, we have the points ( x,y ) = ( -2,3 ) and ( 2,5 ). Substituting these in the general form gives us,

4a - 2b + 3 = 3 → 4a - 2b = 0 → b = 2a.

4a + 2b + 3 = 5 → 4a + 2b = 2 → 2a + b = 1 → 2a + 2a = 1 ( As, b = 2a ) → 4a = 1 →
`a=(1)/(4)`.

So,
`b=(1)/(2)`.

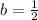Therefore, the equation of the parabola obtained is
`y=(x^(2))/(4)+(x)/(2)+3`.

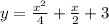The graph of this function is given below and we can see from the graph that domain contains all real numbers and the range is
`y\geq -1`.

Hence, in the interval form we get,

Domain is
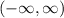`( -\infty,\infty )` and Range is
`[ -1,\infty )`