Question

Solve the quadratic equation by completing the square.

2x² - 20x + 48 = 0

Answer 1

Answer: x = 4 x = 6

Explanation:

2x² - 20x + 48 = 0

2x² - 20 x + _____ = -48 + ______ subtracted 48 from both sides

2(x² - 10x + _____ ) = 2(-24 + _____ ) factored out 2 from both sides

x² - 10x + _____ = -24 + _____ divided both sides by 2

x² - 10x + 25 = -24 +25 added 25 to both sides

↓ ↑ ↑

`(-10)/(2)=(-5)^2`
`\bigg((b)/(2)\bigg)^2` makes a perfect square

(x - 5)² = 1 simplified

`√((x-5)^2) =√(1)` took square root of both sides

x - 5 = ± 1 simplified

x - 5 = 1 x - 5 = -1 split into two separate equations

x = 6 x = 4 solved for x

Answer 2

Steps

So firstly, we need to isolate the x terms onto one side. To do this, subtract 48 on both sides of the equation:

`2x^2-20x=-48`

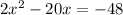
Next, divide both sides by 2:

`x^2-10x=-24`

Next, we are gonna make the left side of the equation a perfect square. To find the constant of this soon-to-be perfect square, divide the x coefficient by 2 and then square the quotient. Add the result onto both sides of the equation:

`-10 / 2=-5\\(-5)^2=25\\\\x^2-10x+25=1`

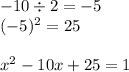
Now, factor the left side:

`(x-5)^2=1`

Next, square root both sides of the equation:

`x-5=\pm 1`

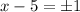
Next, add 5 to both sides of the equation:

`x=5\pm 1`

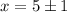
Lastly, solve the left side twice -- once with the plus sign and once with the minus sign.

`x=6,4`

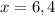
Answer

In short, x = 6 and 4