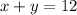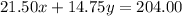Question

A local amusement park charges $21.50 per daily adult ticket and $14.75 per daily child's ticket. A group of 12 people paid $204.00 for tickets. Which system of equations could be used to find x, the number of adult tickets purchased, and y, the number of children's tickets purchased

Answer 1

`x+y = 12`

`21.50x+14.75y=204.00`

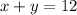
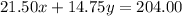
Explanation:

Given :

A local amusement park charges $21.50 per daily adult ticket and $14.75 per daily child's ticket.

Group of 12 people paid $204.00 for tickets.

To Find : System of equations could be used to find x, the number of adult tickets purchased, and y, the number of children's tickets purchased.

Solution :

Since group contains 12 people so no. of tickets are 12 .

Let out of 12 people no. of adults's tickets are x.

Let out of 12 people no. of children's ticket are y .

⇒
`x+y = 12`

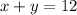
Since charge of one adult ticket = $21.50

So, charge of x adult tickets = $21.50 x

Since charge of one child ticket = $14.75

So, charge of y children tickets =$14.75 y

And we are given that total amount paid by these 12 people = $204.00

Thus
`21.50x+14.75y=204.00`

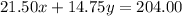
Hence , System of equations could be used to find x, the number of adult tickets purchased, and y, the number of children's tickets purchased:

`x+y = 12`

`21.50x+14.75y=204.00`

Answer 2

`x+y=12`

`21.50x+14.75y=204`

Explanation:

Let x be the number of adult tickets and y be the number of children's tickets.

We are given that there are total 12 people. Therefore, we can set:

`x+y=12`

Moreover, we are given that an adult ticket costs $21.50 and a child's ticket costs $14.75, therefore, cost of x adult tickets will be
`21.50x` and cost of y children's ticket will be
`14.75y`. We can form the second equation by setting the total cost of tickets as:

`21.50x+14.75y=204`

Therefore, the required system of equations that could be used to find x and y will be:

`x+y=12`

`21.50x+14.75y=204`