Answer:
System of equations :
$111.25=$9x+$8y
$33.25=$3x+$2y
The cost of 1 drink = $x = $7.25
The cost of 1 popcorn bag = $y = $5.75
Explanation:
Given :
Naomi spends a total of $111.25 on 9 drinks and 8 bags of popcorn.
Sofia spends a total of $33.25 on 3 drinks and 2 bags of popcorn.
To Find : A system of equations that can be used to find the price of one drink and the price of one bag of popcorn.
Solution :
Let cost of 1 drink = $x
⇒ cost of 9 drinks = $9x
⇒ cost of 3 drinks = $3x
Let cost of 1 popcorn bag = $y
⇒Cost of 8 popcorn bags = $8y
⇒Cost of 2 popcorn bags = $2y
Since Naomi spends a total of $111.25 on 9 drinks and 8 bags of popcorn.
So, equation will be : $111.25=$9x+$8y --(A)
Since, Sofia spends a total of $33.25 on 3 drinks and 2 bags of popcorn.
So, equation will be : $33.25=$3x+$2y--(B)
SOLVING A and B by using substitution method
finding value of x from equation B :
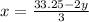
Putting this value in Equation (A)
⇒
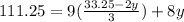
⇒
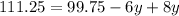
⇒
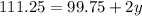
⇒
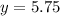
Thus, cost of 1 popcorn bag =y = $5.75
Now put this value of y in equation A to get value of x
⇒$111.25=$9x+$8(5.75)
⇒$111.25-$46 = 9x
⇒$65.25 = 9x
⇒65.25/9 = x
⇒$7.25 = x
Thus, The cost of 1 drink = $x = $7.25