Question

Eric made two investments: Investment Q Q has a value of $ 5 0 0 $500 at the end of the first year and increases by $ 4 5 $45 per year. Investment R R has a value of $ 4 0 0 $400 at the end of the first year and increases by 1 0 % 10% per year. Eric checks the value of his investments once a year, at the end of the year. What is the first year in which Eric sees that investment R R's value exceeded investment Q Q's value?

Answer 1

Answer: it’s 10 I’m 100% sure

Answer 2

Answer: After 8 year from the first year Eric will see that investment R's value exceeded investment Q's value.

Explanation:

Let after x year from the first year Eric sees that investment R's value exceeded investment Q's value.

Investment Q has a value of $ 500 at the end of the first year and increases by $ 45 per year.

Thus, after x year from the first year the total amount of Investment Q,

500 + 45 x

Similarly, after x year from the first year the total amount of Investment R,

⇒
`400(1+(10)/(100) )^x = 400(1.1)^x`

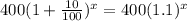
Thus,
`500 + 45 x = 400(1.1)^x`

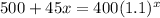
By plotting the equations in the graph,

We get, x = -6.178 or 8.069

But year can not be negative,

Therefore, x = 8.069

Thus, Approx after 8 year from the first year Eric will see that investment R's value exceeded investment Q's value.