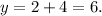Question

In 4 years, Harry’s age will be the same as Jim’s age is now. In 2 years, Jim will be twice as old as Harry will be. Find their ages now.

Harry is _ years old, and Jim is _ years old.

Please Help!

Answer 1

Harry is 2 years old and Jim is 6 years old.

Explanation:

set up the equations. let harry be h and jim be j.

h+4=j

j+2=2(h+2)

plug in the j from the first equation.

you should get h=2 (harry is two years old)

if h+4=j, 2+4=j. so j=6 (jim is six years old)

Answer 2

Harry is 2 years old and Jim is 6 years old.

Explanation:

Let x years be Harry's age now and y years be Jim's age now.

1. In 4 years, Harry’s age will be x+4 years. If in 4 years, Harry’s age will be the same as Jim’s age is now, then

`x+4=y.`

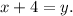
2. In 2 years, Jim's age will be y+2 years and Harry's age will be x+2 years. If in 2 years, Jim will be twice as old as Harry will be, then

`y+2=2(x+2).`

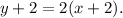
Solve the system of two equations:

`\begin{array}{l}x+4=y\\y+2=2(x+2).\end{array}`

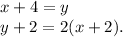
Substitute y=x+4 into the second equation:

`x+4+2=2(x+2),\\ \\x+6=2x+4,\\ \\6-4=2x-x,\\ \\x=2`

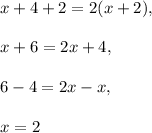
and
`y=2+4=6.`