Answer:
(- 3, 0), (2 +
 , 0), (2 -
, 0), (2 -
 , 0)
, 0)
Explanation:
rearrange the equation equating to zero
x³ - x² - 10x + 6 = 0
note that when x = - 3
(- 3)³ - (- 3)² - 10(- 3) + 6 = - 27 - 9 + 30 + 6 = 0, hence
x = - 3 is a root and (x + 3) is a factor of the polynomial
dividing x³ - x² - 10x + 6 ÷ (x + 3) gives
(x + 3)(x² - 4x + 2) = 0
solve x² - 4x + 2 = 0 using the quadratic formula
with a = 1, b= - 4 and c = 2
x = (4 ±
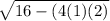 )/ 2
)/ 2
= (4 ±
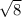 ) / 2
) / 2
= (4 ± 2
 ) / 2
) / 2
= 2 ±
 , hence
, hence
x = 2 +
 , x = 2 -
, x = 2 -

intersect at (- 3, 0), (2 +
 , 0), (2 -
, 0), (2 -
 , 0)
, 0)