Answer:
a(n) = 130 + (n-1) 13
13th term = 286
Explanation:
We are given a sequence of numbers: 130, 143, 156, 169, ... and we are to write an explicit formula to represent the arithmetic sequence and use it to find the 13th term.
We know that the arithmetic sequence can be defined by:
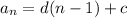
where
 = the common difference between consecutive terms ; and
= the common difference between consecutive terms ; and
 =
=
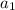
13th term:
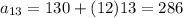
Therefore, the formula for this sequence will be a(n) = 130 + (n-1) 13 and 13th term is 286.