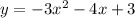Question

Write the equation of the parabola in standard form that passes through the points (0, 3), (1, -4), and (-1, 4).

Answer 1

Steps

• Standard Form of a Parabola: y = ax² + bx + c (a ≠ 0)

So with the three points that are given to us, we will plug them into the standard form formula that I had mentioned earlier. Firstly, plug (0,3) into the equation since the 0 will cancel out the a and b variable:

`3=a*0^2+b*0+c\\3=c`

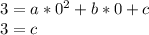
Now we know that the value of c is 3.

Next, plug (1,-4) into the standard form formula and simplify (Remember to plug 3 into the c variable):

`-4=a*1^2+1*b+3\\-4=a+b+3\\-7=a+b`

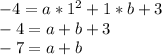
Next, plug (-1,4) into the standard form formula and simplify:

`4=a*(-1)^2+b*(-1)+3\\4=a-b+3\\1=a-b`

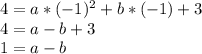
With the last two simplified equations, we will create a system of equations:

`-7=a+b\\1=a-b`

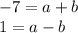
With this, I will be using the elimination method. Add the two equations together, and the following equation is the result:

`-6=2a`

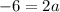
From here we can solve for a. For this, just divide both sides by 2:

`-3=a`

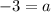
Now that we have the value of a, plug it into either equation to solve for b:

`-7=-3+b\\-4=b\\\\1=-3-b\\4=-b\\-4=b`

Answer

Now, plug the obtained values in our standard form equation and your final answer will be:

`y=-3x^2-4x+3`

Answer 2

`y = -3x^2-4x+3`

Step-by-step explanation

The standard form of a parabola is

`y = ax^2 + bx + c,`

where
`a \\e 0`, and
`a,b,c` are real numbers.

If it passes through (0,3) then when x = 0, y = 3 so this means that

`3 = a(0)^2 + b(0) + c \implies c = 3`

so
`y = ax^2 + bx + 3`.

If it passes through (1,-4), then when x = 1, y = -4 so

`\begin{aligned}-4 &= a(1)^2 + b(1) + 3 \\a+b+3 &= -4 \\a+b &= -7 && \text{(I).}\end{aligned}`

If it passes through (-1,4) then when x = -1, y = 4 so

`\begin{aligned}4 &= a(-1)^2 + b(-1) + 3 \\a-b+3 &= 4 \\a-b &= 1 && \text{(II).}\end{aligned}`

Because both (I) and (II) need to be satisfied, we have the system of equations,

`\begin{cases}a+b &= -7\qquad\text{(I)}\\a-b &= 1\qquad\text{(II)}\end{cases}`

which we can easily solve by adding the two equations up to get

`\begin{aligned}(a+a) + (b-b) &= -7 + 1 \\ 2a&= -6 \\a &= -3.\end{aligned}`

Then we take any of the previous equations to solve for b:

`\begin{aligned}a+b &= -7\\-3 + b &= -7 \\ b &= -4\end{aligned}`

Thus the parabola in standard form is

`y = -3x^2-4x+3.`