Answer: 7
Explanation:
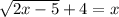
 subtracted 4 from both sides
subtracted 4 from both sides
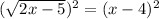 squared both sides to eliminate square root
squared both sides to eliminate square root
2x - 5 = x² - 8x + 16 expanded right side
0 = x² - 10x + 21 subtracted 2x and added 5 on both sides
0 = (x - 3) (x - 7) factored right side
0 = x - 3 0 = x - 7 applied zero product property
x = 3 x = 7 solved for x
Check:
x = 3
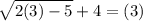
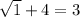
1 + 4 = 3
FALSE! x = 3 is NOT a valid solution
x = 7
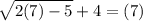
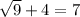
3 + 4 = 7
TRUE! x = 7 IS a valid solution