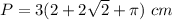Question

For the figures below, assume they are made of semicircles, quarter circles and squares. For each shape, find the area and perimeter. Give your answer as a completely simplified exact value in terms of π (no approximations).

Answer 1

Part a) The area of the figure is
`(9)/(2)(4+\pi )\ cm^(2)`

Part b) The perimeter of the figure is
`3(2+2√(2)+ \pi)\ cm`

Explanation:

Step 1

Find the area of the figure

In this problem we have that

The figure ABC is the half of a square and the other figure is a semicircle

Find the area of the figure ABC

we have

`AB=6\ cm, BC=6\ cm`

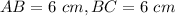
The area of the half square ABC is equal to find the area of triangle ABC

so

`A1=(1)/(2)*6*6=18\ cm^(2)`

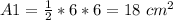
Find the area of the semicircle

The area of the semicircle is equal to

`A2=\pi r^(2)/2`

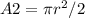
we have that

`r=6/2=3\ cm`

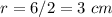
substitute

`A2=\pi (3)^(2)/2`

`A2=(9/2) \pi\ cm^(2)`

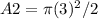
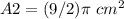
The area of the figure is equal to

`18\ cm^(2)+(9/2) \pi\ cm^(2)= (9)/(2)(4+\pi )\ cm^(2)`

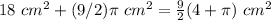
Step 2

Find the perimeter of the figure

The perimeter of the figure is equal to

`P=AB+AC+length\ CB`

we have

`AB=6\ cm`

Applying Pythagoras theorem

`AC=\sqrt{6^(2)+6^(2)}\\AC=6√(2)\ cm`

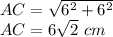
Remember that

the circumference of a semicircle is equal to

`C=(1)/(2)2\pi r=\pi r`

`r=6/2=3\ cm`

`C=\pi(3)`

`C=3 \pi\ cm`

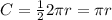
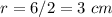
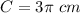
The perimeter of the figure is equal to

`P=6\ cm+6√(2)\ cm+3 \pi\ cm`

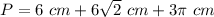
Simplify

`P=3(2+2√(2)+ \pi)\ cm`