Answer:
1.
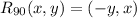
2.

3.
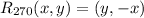 .
.
Explanation:
Let us assume a point (x,y) in the co-ordinate plane on which the transformations will be applied.
Now, we know that 'rotation' is a transformation that turns that image to a certain degree about a point.
So, the given transformations gives us the forms as:
1. When we rotate an ( x,y ) by 90° about origin counter-clockwise, the resultant co-ordinate is ( -y,x ).
So, the function form is
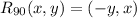 .
.
2. When we rotate an ( x,y ) by 180° about origin counter-clockwise, the resultant co-ordinate is ( -x,-y ).
So, the function form is
 .
.
3. When we rotate an ( x,y ) by 270° about origin counter-clockwise, the resultant co-ordinate is ( y,-x ).
So, the function form is
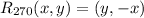 .
.