Question

When f(x) = x-7/2 , what is the value of (f^0 f^-1) (3)

Answer 1

`(f o f^(-1))(3) = 3`

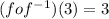
Explanation:

`f(x) = (x-7)/(2)`

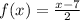
We need to find (fof^-1)(3)

First we find f^-1(x)

Replace f(x) with y

`y = (x-7)/(2)`

Now replace x with y and y with x

`x = (y-7)/(2)`

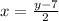
Multiply by 2 on both sides

2x = y -7

Now add 7 on both sides

2x + 7 = y

Replace y with f^-1(x)

f^-1(x) = 2x+ 7

Now we find (fof^-1)(3)

`(f o f^(-1))(3) = f(f^(-1)(3))`

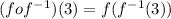
First we find f^-1(3)

f^-1(x) = 2x+ 7

f^-1(3) = 2(3) + 7 = 6 + 7 = 13

Now we plug in 13 for x and find out f(13)

`f(x) = (x-7)/(2)`

`f(13) = (13-7)/(2)= 3`

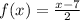
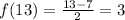
So ,
`(f o f^(-1))(3) = f(f^(-1)(3))= 3`