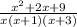--First we have to simplfy
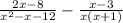
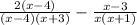
--Cancel common factors
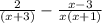
--Here remember never cancel factors in a subtraction or addition problem
--Now Multiply each side until both denominators are equal to each other
![(2[x(x+1)])/(x(x+3)(x+1)) -((x-3)(x+3))/(x(x+3)(x+1))](https://img.qammunity.org/2019/formulas/mathematics/high-school/uu5usbpbrnveeir5n9co6iorgkrhexin80.png)
--Simplify
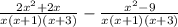
--Now that the denominators are the same: subtract!
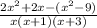
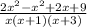
--And LAST STEP! ......Simplify More.... To get your answer