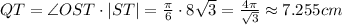Question

Figure 6 shows a semicircle PTS with center O and radius 8cm. QST is a sector of a circle with center S and R is the midpoint of OP.

[use=3.142]
Calculate
(a)<TOR, in radian
(b) length, in cm, TQ curve
PLS HELP MEEE
THNKYU

Answer 1

(a) <TOR=pi/3 radians

To determine <TOR we use the fact that in the right-angled triangle ORT we know two sides:

|OT|=radius=8cm and |OR|=radius/2=4cm

and can use the sine:

`\sin \angle OTR=(r/2)/(r)=(1)/(2)\implies \angle OTR =(\pi)/(6)`

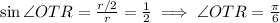
and since <TRO=pi/2, it must be that

`\angle TOR =\pi-(\pi)/(2)-(\pi)/(6)=(\pi)/(3)`

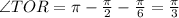
(b) The arc length is approximately 7.255 cm

In order to calculate the arc length QT, we need to first determine the length |ST| and the angle <OST.

Towards determining angle <OST:

`\angle SOT = \pi - \angle TOR = \pi - (\pi)/(3) = (2)/(3)\pi`

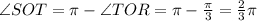
Next, draw a line connecting P and T. Realize that triangle PTS is right-angled with <PTS=pi/2. This follows from the Thales theorem. Since R is a midpoint between P and O, it follows that the triangles ORT and PRT are congruent. So the angles <PTR and <OTR are congruent. Knowing <PTS we can determine angle <OTS:

`\angle OTR \cong \angle PTR=(\pi)/(6)\implies\angle OTS=\angle PTS -\angle PTR -\angle OTR\\\angle OTS = (\pi)/(2)-(\pi)/(6)-(\pi)/(6)=(\pi)/(6)`

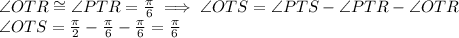
and so the angle <OST is

`\angle OST = \pi - \angle TOS - \angle OTS = \pi -(2)/(3)\pi - (1)/(6)\pi=(\pi)/(6)`

Towards determining |TS|:

Use cosine:

`\cos \angle OST =(|RS|)/(|ST|)\implies |ST|=((3)/(2)r)/(\cos (\pi)/(6))=(12\cdot 2)/(√(3))=8√(3)cm`

Finally, we can determine the arc length QT:

`QT = {\angle OST}\cdot |ST|=(\pi)/(6)\cdot 8 √(3)=(4\pi)/(√(3))\approx 7.255cm`