Answer: x < 3
Explanation:
NOTE:
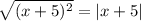
Rewrite the equation:
| x + 5 | < | x + 1 |
Remember that absolute value makes the "inside" value positive, so we need to solve for 2 case of x + 5 (inside is positive or negative) and 2 cases of x + 1.
± (x + 5) < ± (x + 1)
Case 1: + +
x + 5 < x + 1
5 < 1
FALSE
Case 2: - -
-(x + 5) < -(x + 1)
x + 5 > x + 1 divided both sides by -1
5 > 1
TRUE so this works when both "insides" are negative
⇒ x + 5 < 0 and x + 1 < 0
x < -5 and x < -1
since it has to satisfy both, x < -5
Case 3: + -
x + 5 < -(x + 1)
x + 5 < -x - 1 distributed -1 on right side
2x + 5 < -1
2x < -6
x < -3
Case 4: - +
-(x + 5) < x + 1
-x - 5 < x + 1 distributed -1 on left side
-5 < 2x + 1
-6 < 2x
-3 < x
x > -3
This is a contradiction of Case 3 so need to choose a test point.
TEST POINTS (I choose -6, -4, and -2)
| -6 + 5 | < | -6 + 1 |
| -1 | < | -5 |
1 < 5
TRUE so x < -5 is valid
| -4 + 5 | < | -4 + 1 |
| 1 | < | -3 |
1 < 3
TRUE so x < -3 is valid
| -2 + 5 | < | -2 + 1 |
| 3 | < | -1 |
3 < 1
FALSE so x > 3 is NOT valid
Note that x < -3 includes all the values of x < -5, so x < -3 is the answer.
*******************************************************************************
This is a faster way to solve it. Thank you @proner26 !
| x + 5 | < | x + 1 |
(| x + 5 |)² < (| x + 1 |)²
x² + 10x + 25 < x² + 2x + 1
10x + 25 < 2x + 1
8x + 25 < 1
8x < -24
x < -3
Answer: x < -3