You probably already have an idea of what a matrix is; it's a rectangular array of numbers. What they represent is a bit complicated to explain. There's a whole subject about it (see "linear algebra" for more info). Whatever they represent isn't important though, you don't need to know everything about matrices to compute their product (or whether it's even possible).
A quick definition: A matrix of dimension
 -by-
-by-
 is a matrix with
is a matrix with
 rows and
rows and
 columns.
columns.
Matrix multiplication all comes down to an operation called the "dot product". It's defined by the sum of component-wise products of elements between two lists. What this means is, if
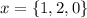 and
and
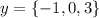 , then the dot product of
, then the dot product of
 and
and
 is
is
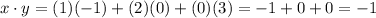
What we did was take the first elements of each list and multiplied them, and the same for the other two elements, then added them all together. Notice that the product can't be computed if
 and
and
 don't thave the same number of elements.
don't thave the same number of elements.
We write this product in matrix form as

Notice the pattern here: on the left, a matrix with 1 row and 3 columns; on the right, a matrix with 3 rows and 1 column. The number of columns of the first matrix have to match the number of rows of the second.
The orientation makes a big difference. The product above returns a 1-by-1 matrix (or simply a scalar number):

On the other hand, the alternate orientation would result in a 3-by-3 matrix.

So the number of rows of the first matrix and number of columns of the second matrix determine the number of rows and columns, respectively, of the matrix product.
I think we have enough information about matrix multiplication to answer this question. If
 has dimensions
has dimensions
 and
and
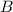 has dimensions
has dimensions
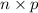 , then the matrix product
, then the matrix product
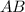 exists (
exists (
 columns in
columns in
 ,
,
 rows in
rows in
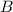 ), but the matrix product
), but the matrix product
 does not (
does not (
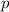 columns in
columns in
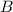 ,
,
 rows in
rows in
 , but
, but
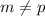 ). So I is not true.
). So I is not true.
We know
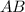 exists, and with
exists, and with
 rows in
rows in
 and
and
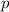 columns in
columns in
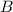 , we expect
, we expect
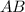 to have
to have
 rows and
rows and
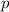 columns, so
columns, so
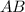 has dimensions
has dimensions
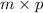 . So II is true.
. So II is true.
With dimensions
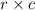 , a matrix would contain
, a matrix would contain
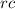 elements.
elements.
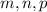 are distinct, so
are distinct, so
 . So III is not true.
. So III is not true.