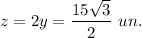Answer:
a=3.75 un., b=11.25 un.
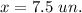

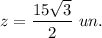
Explanation:
Given triangle is special 30°-60°-90° right triangle. The leg that is opposite to the angle of measure 30° is always equal to half of the hypotenuse. The hypotenuse is of length 15 units, the leg that is opposite to the 30° angle is leg with length of x units, then
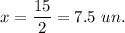
In right triangle with hypotenuse x and legs y and a, angle opposite to the leg a is 30°, then
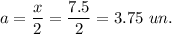
and

By the Pythagorean theorem,
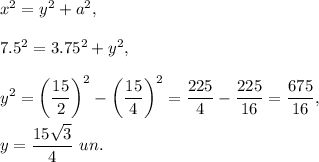
In right triangle with legs y and b and hypotenuse z, leg y is opposite to 30° angle, then