Question

write an equation of the line containing the specified point and perpendicular to indicated line. (-5,6) 4x-y=3

Answer 1

Greetings!

Answer:

y =
`(1)/(2)x + (29)/(4)`

Explanation:

First, we need to rearrange the equation to make it y = mx + c

4x - y = 3

y + 3 = 4x

y = 4x -3

So the slope of the line is 4.

The slope of a line perpendicular to an equation is:

`(-1)/(gradient)`

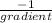
So the slope of the perpendicular line is:

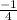`(-1)/(4)` = -0.25

Now to find the equation of a line you can use the following equation:

y - y₁ = m(x - x₁)

Where y₁ is the y-coordinate, x₁ is the x-coordinate and m is the gradient. Plug the values in:

y₁ = 6

x₁ = -5

m =
`(-1)/(4)`

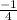
y - 6 =
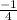`(-1)/(4)`(x - - 5)

To get rid of the fraction we need to multiply the whole equation by 4:

4y - 24 = -1(x - - 5)

The two negatives cancel out:

4y - 24 = -1(x + 5)

Multiply the brackets out:

4y - 24 = -x + 5

Now, to rearrange the formula back into y = mx + c

Move the -24 over to the other side making it a +24:

4y = 2x + 5 + 24

4y = 2x + 29

Divide everything by 4:

y =
`(2)/(4)x + (29)/(4)`

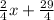
y =
`(1)/(2)x + (29)/(4)`

Hope this helps!