Question

Solve the following systems by Elimination

1) 4x+6y=32
3x-6y=3

2) -3+5y=-11
3x+7y=-1

Answer 1

The solutions for both system of equations are as follows:

1. (5,2)
2. (2,-1)

Explanation:

The first set of equations is:

`4x+6y=32\\3x-6y=3\\`

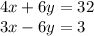
It can clearly be seen that the coefficients of y are already same in magnitude with different signs so we have to add both equations

So adding both equations, we get

`4x+6y+3x-6y = 32+3\\7x = 35\\(7x)/(7) = (35)/(7)\\x = 5`

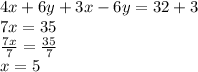
Putting x=5 in equation 1

`4(5)+6y = 32\\20+6y = 32\\6y = 32-20\\6y = 12\\(6y)/(6) = (12)/(6)\\y = 2`

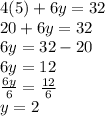
The solution is (5,2)

The second set of simultaneous equations is:

`-3x+5y=-113x+7y=-1`

We can see that the coefficients of x in both equations are same in magnitude with opposite signs so

Adding both equations

`-3x+5y+3x+7y = -11-1\\12y = -12\\(12y)/(12) = (-12)/(12)\\y = -1`

Putting y= -1 in first equation

`-3x+5(-1)=-11\\-3x-5=-11\\-3x=-11+5\\-3x=-6\\(-3x)/(-3) = (-6)/(-3)\\x = 2`

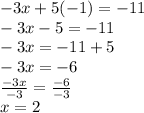
The solution is: (2,-1)

Hence,

The solutions for both system of equations are as follows:

1. (5,2)
2. (2,-1)