1 Answer

XOneca · Answer 1 · 2019-02-24T23:23:00+0000

I'll abbreviate
$s=\sin\theta$ and
$c=\cos\theta$ , so the identity to prove is

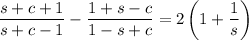
$(s+c+1)/(s+c-1)-(1+s-c)/(1-s+c)=2\left(1+\frac1s\right)$

On the left side, we can simplify a bit:

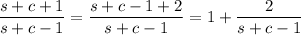
$(s+c+1)/(s+c-1)=(s+c-1+2)/(s+c-1)=1+\frac2{s+c-1}$

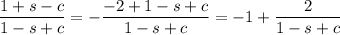
$(1+s-c)/(1-s+c)=-(-2+1-s+c)/(1-s+c)=-1+\frac2{1-s+c}$

Then

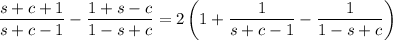
$(s+c+1)/(s+c-1)-(1+s-c)/(1-s+c)=2\left(1+\frac1{s+c-1}-\frac1{1-s+c}\right)$

So the establish the original equality, we need to show that

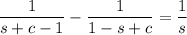
$\frac1{s+c-1}-\frac1{1-s+c}=\frac1s$

Combine the fractions:

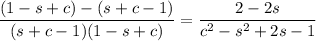
((1-s+c)-(s+c-1))/((s+c-1)(1-s+c))=(2-2s)/(c^2-s^2+2s-1)

We can rewrite the denominator as

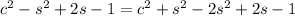
c^2-s^2+2s-1=c^2+s^2-2s^2+2s-1

then using the fact that
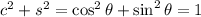$c^2+s^2=\cos^2\theta+\sin^2\theta=1$ , we get

1-2s^2+2s-1=2s-2s^2

so that we have

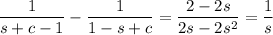
$\frac1{s+c-1}-\frac1{1-s+c}=(2-2s)/(2s-2s^2)=\frac1s$

as desired.

Please log in or register to add a comment.