Question

guys I really need help with part c) I literally have no idea how to this. given that tan(pi/8)=sqrt(2)-1. I am really looking forward to step-by-step explanation.

Answer 1

`c)\\\tan\left((\pi)/(8)\right)=\tan\left(\pi-(7\pi)/(8)\right)=\tan\left(-(7\pi)/(8)\right)=-\tan\left((7\pi)/(8)\right)\\\\=-(1-\sqrt2)=\sqrt2-1\\\\y=\sin(2x-1)+a\tan(\pi)/(8)\\\\\text{We know}\ -1\leq\sin(2x-1)\leq1.\\\\y\geq0\ \text{therefore}\ a\tan(\pi)/(8)\geq1\\\\\text{We have to move the graph at least one unit up}\\\\a(\sqrt2-1)\geq1\qquad\text{divide both sides by}\ (\sqrt2-1)>0\\\\a\geq(1)/(\sqrt2-1)\cdot(\sqrt2+1)/(\sqrt2+1)\\\\a\geq(\sqrt2+1)/((\sqrt2)^2-1^2)`

`a\geq(\sqrt2+1)/(2-1)\\\\a\geq(\sqrt2+1)/(1)\\\\a\geq\sqrt2+1\\\\Answer:\ \boxed{a=\sqrt2+1}`

Answer 2

`a \geq (1)/(√(2) -1)`

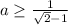
Explanation:

This equation is more intimidating than the problem you have to solve.

You know that the sine of everything is always between -1 and +1. So for the entire expression to be >= 0, the a*tan(pi/8) bit has to be 1 at least. Given this, we can forget about the sin(...) term of the equation for the remainder of solving it.

You already figured out that tan(pi/8) is sqrt(2)-1.

So what we're saying is a * (sqrt(2) - 1) has to be 1 at least.

If we solve a(sqrt(2)-1) >= 1 for a we get:

a = 1/(sqrt(2)-1)