Question

Someone please help!!!

A company is selling two types of treadmills. Treadmill x sells for $750 and treadmill y sells for $900. Three times the number of treadmill y sold must be less than or equal to twice the number of treadmill x sold. The company has at most 100 treadmills to sell. What is the maximum revenue that the company can make from the treadmill sales?


$75,000


$81,000


$84,000


$90,000

Answer 1

Option B is correct

The maximum revenue that the company can make from the treadmill sales is, $81,000

Explanation:

Let x represent the number of treadmill x sold and y represents the number of treadmill y sold

As per the statement: Three times the number of treadmill y sold must be less than or equal to twice the number of treadmill x sold.

⇒
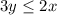`3y\leq 2x` ......[1]

Also, it is given that the company has at most 100 treadmills to sell.

⇒
`x+y\leq 100`

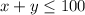
using a graph tool for equation [1] and [2] as shown in figure given below;

⇒ the solution is the shaded area

The maximum revenue that the company can make is for the point, (60, 40)

⇒ x = 60 treadmills

and y = 40 treadmills

Maximum Revenue =
`60 * 750 + 40 * 900 = 45000+36000 = \$81,000`

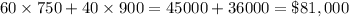
Therefore, the maximum revenue that the company can make from the treadmill sales is, $81,000