Question

Karen uses her credit card to purchase a new television for $695.20. She can pay off up to $325 per month. The card has an annual rate of 17.9% compounded monthly. How much will she pay in interest?

$6.28



$16.96



$20.44



$62.16

Answer 1

Answer: $ 16.96

Explanation:

Here, the present value of the loan, PV = $695.20

Annual Interest rate = 17.9%

⇒ Monthly interest rate = 17.9/12 = 1.41666666667

Thus, the monthly interest rate (decimal ) , r = 0.014167 ( approx)

Monthly payment, P = $ 325

Let the time period of the loan = n.

Since,
`P= (r(PV))/(1-(1+r)^(-n))`

⇒
`325= (0.014167(695.20))/(1-(1+0.014167)^(-n))`

⇒
`1-(1+0.014167)^(-n)= (10.37008984)/(325)`

⇒
`1-(1+0.014167)^(-n)= 0.03190796873`

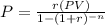
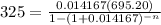
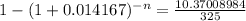
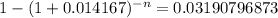
⇒ n = 2.19

Thus, her total payment = 2.19 × 325 = 711.75

⇒ Her total interest = 711.75 - 695.20 = $16.55

Since only 16.96 is near to 16.55

Thus, second option is correct.