Question

A salesperson earns a salary of $700 per month plus 2% of the sales. Which inequality correctly represents the total sales if the salesperson is to have a monthly income of at least $1800?

x ≤ $45,000




x ≤ $55,000




x ≥ $55,000




x ≥ $45,000

Answer 1

C.
`x\geq 55000`

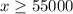
Step-by-step explanation:

Let x be the total monthly sales.

We have been given that a salesperson earns a salary of $700 per month plus 2% of the sales. The salesperson want to have a monthly income of at least $1800.

This means that 700 plus 2% of total monthly sales should be greater than or equal to 1800. We can represent this information in an equation as:

`700+((2)/(100))x\geq 1800`

`700+0.02x\geq 1800`

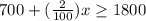
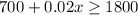
Let us solve our inequality to find the monthly sales (x).

Subtract 700 from both sides of our inequality.

`700-700+0.02x\geq 1800-700`

`0.02x\geq 1100`

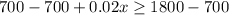
Divide both sides of inequality by 0.02.

`(0.02x)/(0.02)\geq (1100)/(0.02)`

`x\geq (1100)/(0.02)`

`x\geq 55000`

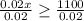
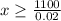
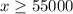
Therefore, the total monthly sales must be greater than or equal to 55,000 and option C is the correct choice.