Answer: a = 1, a =
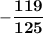
Explanation:
In order to have the same root, the discriminant cannot be irrational.
- Case 1: Discriminant = zero
- Case 2: Discriminant = perfect square
(a + 3)x² - (11a + 1)x + a = 2(a - 5)
(a + 3)x² - (11a + 1)x + a = 2a - 10
(a + 3)x² - (11a + 1)x + a - 2a + 10 = 0
(a + 3)x² - (11a + 1)x - (a - 10) = 0
a = a+3 b = -(11a+1) c = -(a - 10)
Case 1:
b² - 4ac = 0
[-(11a + 1)]² - 4(a + 3)[-(a - 10)] = 0
121a² + 22a + 1 + 4a² - 28a - 120 = 0
125a² - 6a - 119 = 0
Use any method to solve the quadratic equation. I chose to use the factoring method.
125a² - 6a - 119 = 0
125a² - 125a + 119a - 119 = 0
125a(a - 1) + 119(a - 1) = 0
(125a + 119)(a - 1) = 0
125a + 119 = 0 and a - 1 = 0
a =
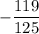 and a = 1
and a = 1
Check:
(a + 3)x² - (11a + 1)x + a = 2(a - 5)
((1) + 3)x² - (11(1) + 1)x + (1) = 2((1) - 5)
4x² - 12x + 1 = -8
4x² - 12x + 9 = 0
(2x + 3)² = 0
x =
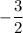
Case 2: I am not sure how to do this one