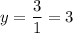Answer: vertical asymptotes: x = 2, x = -2
horizontal asyptote: y = 3
Explanation:
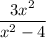
Vertical Asymptotes are the restrictions on "x", which is denoted by the denominator being unequal to zero.
x² - 4 = 0
(x + 2)(x - 2) = 0
x + 2 = 0 and x - 2 = 0
x = -2 and x = -2
Horizontal Asymptotes are determined by the degree of the numerator (n) compared to the degree of the denominator (m) as follows:
- If n > m , then no horizontal asymptote (use long division to find slant asymptote)
- If n = m , then horizontal asymptote is coefficient of n divided by coefficient of m
- If n < m , then horizontal asymptote is: y = 0
In the given problem, the degree of both the numerator and denominator is 2 so horizontal asymptote is: