Question

What is the lateral area of the pyramid?

Answer 1

We have two triangles with base 9ft and height 12.3ft and two triangles with base 11ft and height 11.9ft.

The formula of an area of a triangle:

`A_\triangle=(1)/(2)bh`

Triangle #1:

b = 9ft and h = 12.3ft. Substitute:

`A_1=(1)/(2)(9)(12.3)=55.35ft^2`

Triangle #2:

b = 11ft and h = 11.9ft. Substitute:

`A_2=(1)/(2)(11)(11.9)=65.45ft^2`

The Lateral Area:

`L.A.=2A_1+2_A2\\\\L.A.=2(55.35)+2(65.45)=241.6\ ft^2`

Answer: B. 241.6 ft².

Answer 2

Answer: B

Explanation:

The point here, on calculating the Lateral Area of a Pyramid is searching for Congruent Triangles. In a rectangular pyramid, we have four triangles, in the Lateral Area.

The basic formula for calculating the Area of any triangle is:

Δ
`=(1)/(2)*base*height`

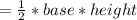
So, let's plug it in the values for the 1st triangle:

Δ
`(1)/(2)* 11*11.9`

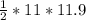
Δarea=
`65.45 ft^(2)`

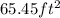
For the second triangle (on the left):

Δ=
`(1)/(2)*9*12.3=\\ 55.35 ft²`

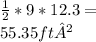
The base is a rectangle, this assures us the base of the other faces is also 9 ft and 11 ft.

So we can assume the other Triangle are congruent to Triangle 1 and 2.

The Lateral Area is the sum of all Pyramid's Triangles area:

55.35+55.35+65.45+65.45=241.6 ft²