Question

4 Questions about The Polynomial Remainder Theorem

Answer 1

None of these questions have anything to do directly with the polynomial remainder theorem. The theorem says that the remainder upon dividing a polynomial
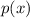`p(x)` by
`x-c` is given by the value of
`f(c)`.

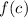For these questions, all you really have to do is evaluate the given polynomials at the given points, and IMO is much less work.

Question 2:
`f(5)=4(5)^2-5(5)+2=77`

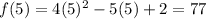
Question 3:
`f(4)=3(4)^4-8)4)^2-2(4)+12=644`

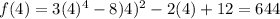
Question 4: Here you have check the value of
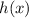`h(x)` and 2 and -2, then interpret them as points in the coordinate plane,
`(x,h(x))`.

`h(-2)=2(-2)^5-4(-2)^4-2(-2)^2+15=-121`

`h(2)=2(2)^5-4(2)^4-2(2)^2+15=7`

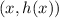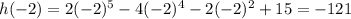
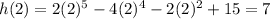
Question 5: Same as in question 4, but you have to check
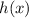`h(x)` at -4, -3, -2, -1.

`h(-4)=72`

`h(-3)=46`

`h(-2)=26`

`h(-1)=12`

- - -

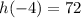
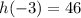
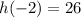
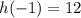
If you insist on using the polynomial remainder theorem, it's a question of polynomial division. For instance, in question 2 you'd compute

`(4x^2-5x+2)/(x-5)=4x+15+(77)/(x-5)\implies4x^2-5x+2=(4x+15)(x-5)+77`

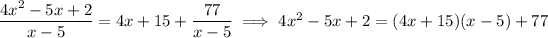
so the remainder is 77, as we found by simply computing
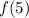`f(5)`.