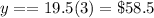Question

A water park offers a season pass for $64 per person which includes free

admission and free parking. Admission for the water park is $14.50 per person. Parking is normally $5 for those without a season pass.

a. How many visits to the water park would you have to use for
the season
pass to be a better deal?

b. What would the total cost be for 3 visits with and without a season pass?

Answer 1

Part a) The number of visits mus be greater than or equal to
`4`

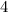
Part b)

with season pass

The total cost is
`\$64`

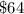
without season pass

The total cost is
`\$58.5`

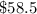
Explanation:

Let

x---> the number of visit to the water park

y---> the total cost to visit the water park per person

we know that

`y=(14.50+5)x=19.5x`

so

Part a) How many visits to the water park would you have to use for the season pass to be a better deal?

For
`y=\$64`

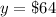
Substitute the value of y in the equation and solve for x

`64=19.5x`

`x=64/19.5=3.28\ visits`

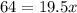
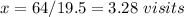
therefore

The number of visits mus be greater than or equal to
`4`

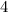
Part b) What would the total cost be for 3 visits with and without a season pass?

with season pass

The total cost is
`\$64`

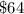
without season pass

The total cost for
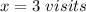`x=3\ visits` is

`y==19.5(3)=\$58.5`