Question

How do the graphs of the function f(x)=(3/2)x and g(x)=(2/3)x compare

Answer 1

The graphs are reflections of each other over the y-axis. The graph of g(x) shows exponential decay, while the graph of f(x) shows exponential growth.

Explanation:

Answer 2

f is a line through 0 and (2,3)

g is a line through 0 and (3,2)

Explanation:

f and g are proportional linear functions. They each have the form y=mx+b where b=0 and m is a fraction. The m or slope tell us the form the function takes on the graph. It is a straight line through 0 with steepness m.

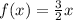`f(x)=(3)/(2) x` has steepness 3/2. Starting at (0,0) or the origin, move up three grid lines on the y-axis and then over 2 grid lines. Mark your point at (2,3). Then connect and draw arrows on the end.

`g(x)=(2)/(3)x` has steepness 2/3. Starting at (0,0) or the origin, move up two grid lines on the y-axis and over 3 grid lines. Mark your point at (3,2). Then connect and draw he arrows on the end.