Answer:
see explanation
Explanation:
the n th term of an arithmetic sequence is
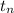 =
=
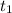 + (n - 1)d
+ (n - 1)d
given
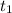 = 3 and
= 3 and
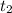 = 10, then
= 10, then
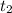 = 3 + d = 10 ⇒ d = 10 - 3 = 7
= 3 + d = 10 ⇒ d = 10 - 3 = 7
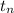 = 3 + 7(n - 1) = 3 + 7n - 7 = 7n - 4
= 3 + 7(n - 1) = 3 + 7n - 7 = 7n - 4
the sum to n terms of an arithmetic sequence is
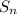 =
=
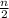 [2
[2
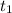 + (n - 1)d ]
+ (n - 1)d ]
=
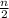 [(2 × 3) + 7(n - 1) ]
[(2 × 3) + 7(n - 1) ]
=
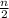 (6 + 7n - 7 )
(6 + 7n - 7 )
=
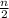 (7n - 1)
(7n - 1)
=
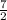 n² -
n² -
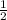 n
n