Answer:
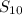 = - 30
= - 30
Explanation:
For a given arithmetic sequence the n th term formula is
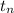 =
=
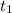 + (n - 1)d
+ (n - 1)d
where d is the common difference and
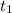 the first term
the first term
We have to find d and
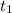
from the given information we can write 2 equations and solve for d and
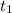
 =
=
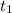 + 5d = - 4 → (1)
+ 5d = - 4 → (1)
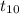 =
=
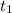 + 9d = - 12 → (2)
+ 9d = - 12 → (2)
subtract (1) from (2) term by term
4d = - 8 ⇒ d = - 2
substitute d = - 2 in (1)
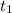 - 10 = - 4 ⇒
- 10 = - 4 ⇒
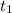 = - 4 + 10 = 6
= - 4 + 10 = 6
The sum to n terms of an arithmetic sequence is
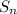 =
=
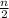 [2
[2
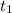 + (n - 1)d ], hence
+ (n - 1)d ], hence
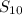 = 5[(2 × 6) + (9 × - 2) ] = 5(12 - 18) = 5 × - 6 = - 30
= 5[(2 × 6) + (9 × - 2) ] = 5(12 - 18) = 5 × - 6 = - 30