Question

Simplify (2p+3)2 - (2p-3)2 (Give proper detailed answer with all steps)

Answer 1

`24p`

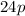
Explanation:

There's a very useful pattern in factoring and multiplying binomials called a difference of squares, and it looks like this:

`(x+y)(x-y)=x^2-y^2`

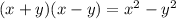
We can use this difference of squares to factor the expression we've been given, setting
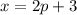`x=2p+3` and
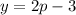`y=2p-3` to obtain the expression

`(2p+3)^2-(2p-3)^2=[(2p+3)+(2p-3)][(2p+3)-(2p-3)]` (1)

tackling each of the multiplicands on the right:

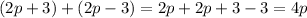`(2p+3)+(2p-3)=2p+2p+3-3=4p` (Left)

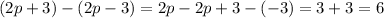`(2p+3)-(2p-3)=2p-2p+3-(-3)=3+3=6` (Right)

This simplifies the expression on the right of (1) to
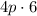`4p\cdot6`, or simply
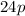`24p`.