Answer:
Yes, the side lengths of ΔABC forms a Pythagorean triple
Explanation:
Given : A right angled triangle ABC
Side lengths - 3,4 and 5
To Find: . Do the side lengths form a Pythagorean triple?
Solution :
Hypotenuse (longest side) = 5
To check we need to use Pythagoras theorem :
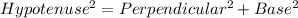
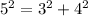
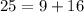
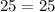
Since Pythagoras theorem is verified . So, the side lengths form the Pythagorean triplet.
Hence the side lengths of ΔABC forms a Pythagorean triple