Question

What is the approximate length of the base of an isosceles triangle if the congruent sides are 3 feet and the vertex angle is 35°?

Answer 1

1.80 feet.

Step-by-step explanation:

Please see the attachment.

Let c be the length of base of our given triangle.

We have been given that an isosceles triangle's congruent sides are 3 feet the vertex angle is 35 degrees. We are asked to find the length of the base of isosceles triangle.

We will use law of cosine to find the length of our base.

`c=\sqrt{a^2+b^2-2ab\text{ Cos(C)}}`

Upon substituting our given values in above formula we will get,

`c=\sqrt{3^2+3^2-2* 3* 3*\text{ Cos(35)}}`

`c=\sqrt{9+9-18*\text{ Cos(35)}}`

`c=√(18-18* 0.819152044289)`

`c=√(18-14.744736797202)`

`c=√(3.255263202798)`

`c=1.8042347970255978\approx 1.80`

Therefore, the length of base of our given isosceles triangle is approximately 1.80 feet.

Answer 2

Properties of isosceles triangle:

• Two sides are congruent(i.,e equal)

• Corresponding angles opposite to these sides are equal.

• A Perpendicular drawn to the third side from the corresponding vertex will bisect the third side.

• Also the altitude drawn will divide the isosceles triangle into two congruent right triangles.

As per the given statement:

Congruent sides(a) = 3 feet And Vertex angle(
`\angle QPR`) =
`35^(\circ)`

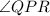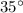
Let the length of the base(QR) of an isosceles triangle PQR be 2b.

By isosceles properties, in triangle PQR , the median of an isosceles triangle from its vertex angle is also the perpendicular bisector of the base.

Also, this line divides the triangle into two congruent right angled triangles whose hypotenuse is 3 feet,

and
`\angle QPS = (\angle QPR)/(2) = (35)/(2) = 17.5^(\circ)`

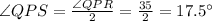
In a right angle triangle QSP

Using sine ratio formula;

`\sin \theta = \frac{\text{opposite side}}{\text{Hypotenuse side}}`

Hypotenuse sides = PQ = 3 ft and Opposite side = QS = b ft

Solve for b using using sine ratio:

`\sin (17.5^(\circ)) = (b)/(3)`

or

`b = 3 \cdot \sin(17.5^(\circ))`

`b = 3 \cdot 0.3007057995`

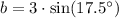
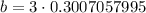
Simplify:

b = 0.902117398

Length of the base of an isosceles triangle PQR = 2b = 2(0.902117398) = 1.8042348

Therefore, the approximate length of the base of an isosceles triangle is, 1.8 feet